无编辑摘要 |
(→单调栈) |
||
| 第3行: | 第3行: | ||
'''栈(Stack)'''是一种'''后进先出(LIFO, Last In First Out)'''的数据结构,栈只有一端能够进出元素,我们通常称这一端为栈顶,另一端为栈底。通常支持3种运算,分别为查看栈顶(top),加入栈(push),和删除栈顶(pop)。 | '''栈(Stack)'''是一种'''后进先出(LIFO, Last In First Out)'''的数据结构,栈只有一端能够进出元素,我们通常称这一端为栈顶,另一端为栈底。通常支持3种运算,分别为查看栈顶(top),加入栈(push),和删除栈顶(pop)。 | ||
== 单调栈 == | == 单调栈<ref>单调栈,OI Wiki</ref> == | ||
单调栈就是满足单调性的栈结构。 | |||
将一个元素插入单调栈时,为了维护栈的单调性,需要在保证将该元素插入到栈顶后整个栈满足单调性的前提下弹出最少的元素。 | |||
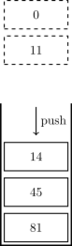
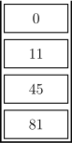
例如,栈中自顶向下的元素为<math>\{0,11,45,81\}</math> | |||
[[File:monotonous-stack-after.svg]] | [[File:monotonous-stack-after.svg]] | ||
插入元素 时为了保证单调性需要依次弹出元素<math>0,11</math> ,操作后栈变为<math>\{14,45,81\}</math>。 | |||
[[File:monotonous-stack-before.svg]] | [[File:monotonous-stack-before.svg]] | ||
2022年2月18日 (五) 16:38的版本
栈(Stack)是一种后进先出(LIFO, Last In First Out)的数据结构,栈只有一端能够进出元素,我们通常称这一端为栈顶,另一端为栈底。通常支持3种运算,分别为查看栈顶(top),加入栈(push),和删除栈顶(pop)。
单调栈[1]
单调栈就是满足单调性的栈结构。
将一个元素插入单调栈时,为了维护栈的单调性,需要在保证将该元素插入到栈顶后整个栈满足单调性的前提下弹出最少的元素。
例如,栈中自顶向下的元素为[math]\displaystyle{ \{0,11,45,81\} }[/math]
插入元素 时为了保证单调性需要依次弹出元素[math]\displaystyle{ 0,11 }[/math] ,操作后栈变为[math]\displaystyle{ \{14,45,81\} }[/math]。
- ↑ 单调栈,OI Wiki